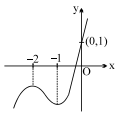
Question

For the cubic, $f(x)=2 x^3+9 x^2+12 x+1$ which one of the following statement, does not hold good?

• A. $f ( x )$ is non monotonic
• B. increasing in $(-\infty,-2) \cup(-1, \infty)$ and decreasing is $(-2,-1)$
• C. $f : R \rightarrow R$ is bijective
• D. Inflection point occurs at $x=-3 / 2$

Answer 1

Answer: (C)

$ f ( x )=2 x ^3+9 x ^2+12 x +1 $
$f ^{\prime}( x )=6\left[ x ^2+3 x +2\right]=( x +2)( x +1)$
$\text { Hence } x =-2 \text { is maxima and } x =-1 \text { is minima }$
$ f ^{\prime \prime}( x )=2 x +3=0$
$\Rightarrow x =-3 / 2 \text { is the inflection point }$
$\text { obviously } f \text { is non monotonic }$
$\therefore f \text { is many one } $
$\text { hence it is not bijective. }$