Q.
For the circuit shown in figure, the emf of the generator is $E$. The current through the inductor is $1.6 \,A$, while the current through the condenser is $0.4 \,A$. Then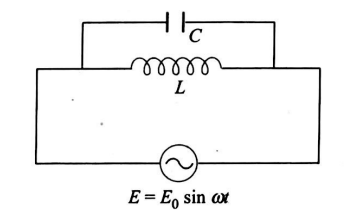
Alternating Current
Solution:
