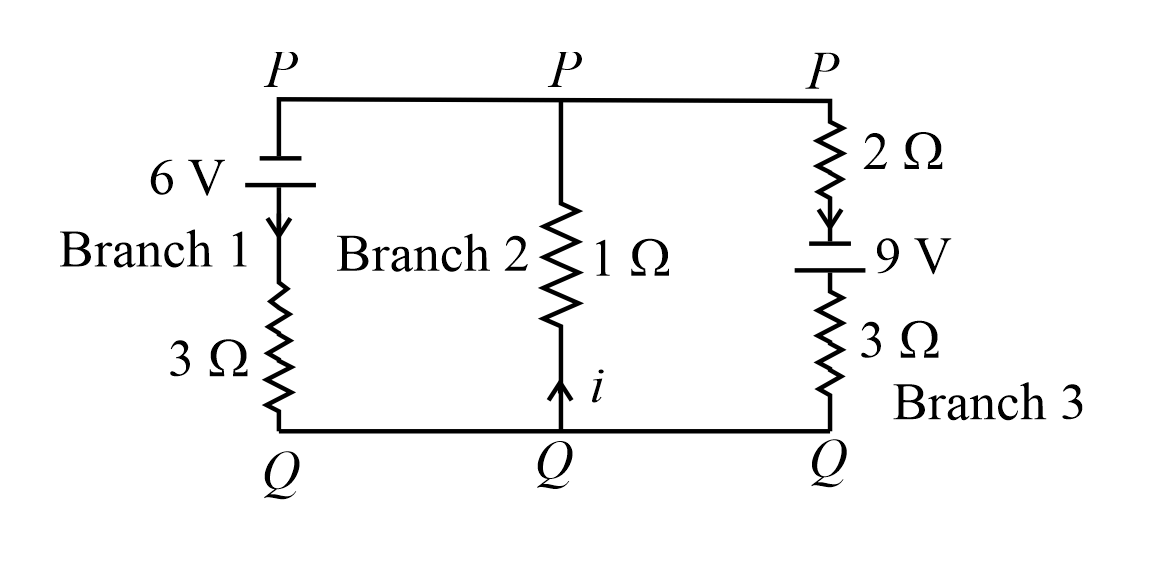
Question

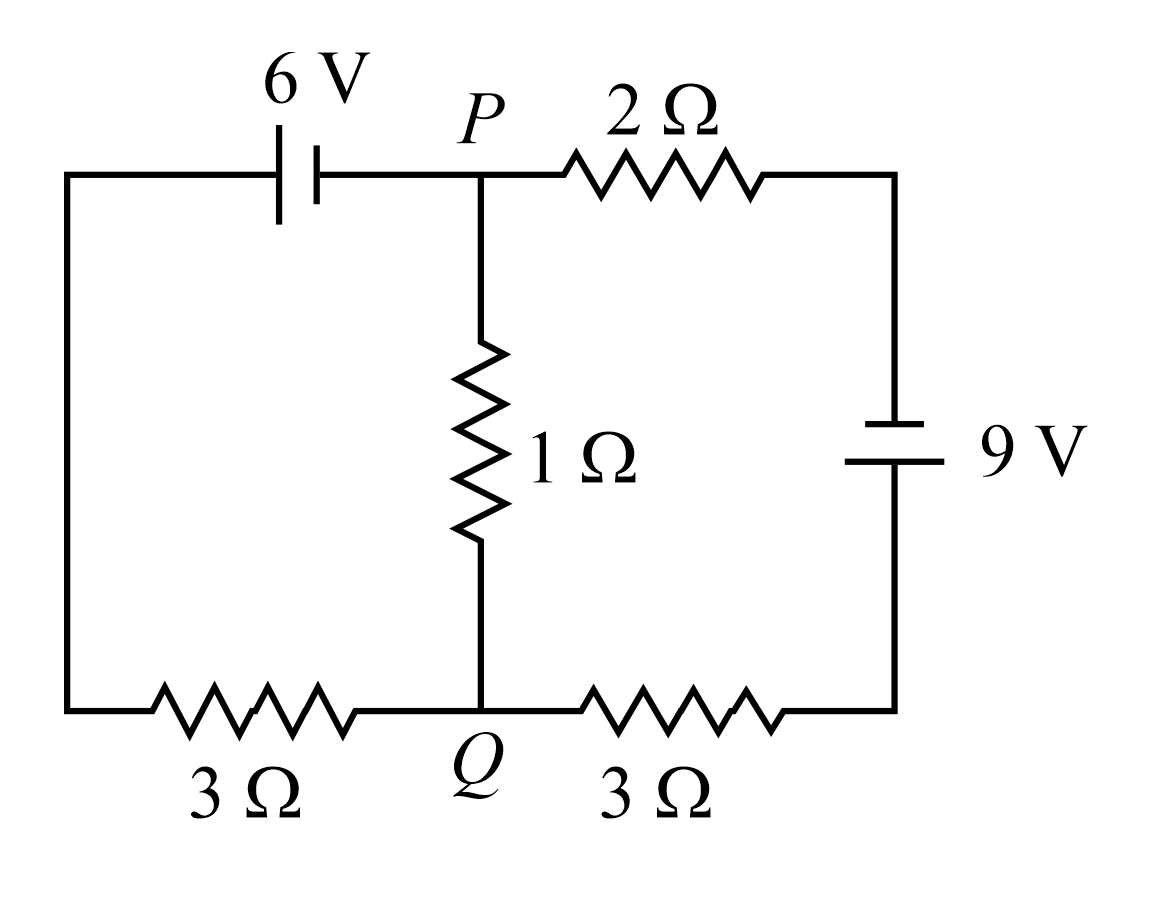
For the circuit given below, if the current in the $1\,\Omega$ resistor is $\frac{x}{23}A$ , what is the value of $x$ ? Assume the batteries are ideal.

Answer 1

The circuit given in the problem can be redrawn as shown below.

The three branches are connected between the same points $P$ and $Q$ and hence they are in parallel. For such a circuit the potential difference between the points $P$ and $Q$ is
$V_{Q P}=\frac{\frac{E_{1}}{R_{1}}+\frac{E_{2}}{R_{2}}+\frac{E_{3}}{R_{3}}}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}}$
Where $E_{1},E_{2}\text{and}E_{3}$ are the emf of the batteries present in the first, second and the third branch.
Similarly, $R_{1},R_{2}\text{and}R_{3}$ are the values of resistance in each of the respective branches.
$V_{Q P}=\frac{\frac{6}{3}+\frac{0}{1}+\frac{9}{5}}{\frac{1}{3}+\frac{1}{1}+\frac{1}{5}}=\frac{57}{23}V$
The value of current through the $1\Omega$ resistance is
$i=\frac{V_{Q P}}{1}=\frac{57}{23}A=2.48A$