Question

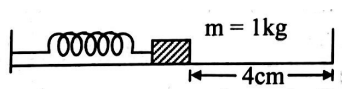
For the arrangement shown in figure, the spring is initially compressed by $3 \,cm$. when the spring is released the block collides with the wall and rebounds to compress the spring again. The maximum compression in the spring after collision (coefficient of restitution is $0.7$ ) is ______$cm$. (Take $\sqrt{5}=2.24, k =10^{4} N / m$ )

Answer 1

From Energy conservation,
$\frac{1}{2} mv _{0}{ }^{2}+\frac{1}{2} kx ^{2}=\frac{1}{2} kx _{0}{ }^{2} $
$\Rightarrow v _{0}=\sqrt{\frac{ k }{ m }\left( x _{0}{ }^{2}- x ^{2}\right)}$
.... [velocity of block just before collision]
Here $x _{0}=0.03 \,m , x =0.01 \,m$,
$k =10^{4} N / m , m =1\, kg$
$v _{0} =\sqrt{\frac{10^{4}}{1}\left[(0.03)^{2}-(0.01)^{2}\right]} $
$=\sqrt{10^{4} \times 10^{-4}[9-1]} $
$=2 \sqrt{2} \,m / s$
After collision, $v = ev _{0}$
$=(0.7) 2 \sqrt{2}$
$=\frac{1}{\sqrt{2}} \times 2 \sqrt{2}$
$=2 \,m / s$
$\cdots$. [ $\because$ Take $0.7 \approx \frac{1}{\sqrt{2}}$ ]
maximum compression in the spring ;
$\frac{1}{2} kx _{ m }^{2} =\frac{1}{2} kx ^{2}+\frac{1}{2} mv ^{2} $
$\Rightarrow x _{ m } =\sqrt{ x ^{2}+\frac{ m }{ k } v ^{2}}$
$=\sqrt{(0.01)^{2}+\frac{1(2)^{2}}{10^{4}}} $
$=\frac{\sqrt{1+4}}{10^{2}}=\frac{2.24}{10^{2}} m $
$\therefore x _{ m } =2.24\, cm$