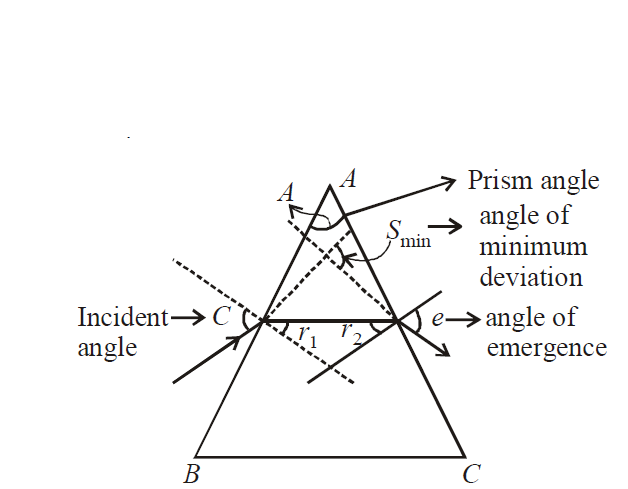
Question

For the angle of minimum deviation of a prism to be equal to its refracting angle, the prism must be made of a material whose refractive index :

• A. lies between $\sqrt {2}$ and $1$
• B. lies between 2 and $\sqrt {2}$
• C. is less then 1
• D. is greater then 2

Answer 1

Answer: (B)

The angle of minimum deviation is given as
$\delta_{\min }=i+e-A$
for minimum deviation
$\delta_{\min }= A $ then
$2 A = i + e$
in case of $\delta_{\min } ; i=e$
$2 A =2 i r _{1}= r _{2}=\frac{ A }{2}$
$ i = A =90^{\circ}$
$1 \sin r = n \sin r _{1} $
$\sin A = n \sin \frac{ A }{2}$
$2 \sin \frac{ A }{2} \cos \frac{ A }{2}= n \sin \frac{ A }{2}$
$2 \cos \frac{ A }{2}= n$
when $A=90^{\circ}=i_{\min }$
then $n_{\min }=\sqrt{2}$
$i=A=0$
$n_{\max }=2$