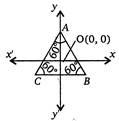
Question

For an equilateral triangle the centre is the origin and the length of altitude is a. Then, the equation of the circumcircle is:

• A. $ {{x}^{2}}+{{y}^{2}}={{a}^{2}} $
• B. $ 3{{x}^{2}}+3{{y}^{2}}=2{{a}^{2}} $
• C. $ {{x}^{2}}+{{y}^{2}}=4{{a}^{2}} $
• D. $ 3{{x}^{2}}+3{{y}^{2}}={{a}^{2}} $
• E. $ 9{{x}^{2}}+9{{y}^{2}}=4{{a}^{2}} $

Answer 1

Answer: (E)

Centre of triangle is (0, 0).
$ \therefore $ Since triangle is an equilateral, the centre of circumcircle is also (0, 0) $ AD=a $ (given)
$ \therefore $ $ AC=BC=AB=\frac{a}{\sin 60{}^\circ }=\frac{2a}{\sqrt{3}} $

$ \therefore $ Circumradius
$=\frac{AC}{2\sin B} $
$=\frac{2a}{\sqrt{3}.2}\times \frac{2}{\sqrt{3}} $ $ (\because B=60{}^\circ ) $
$=\frac{2a}{3} $
$ \therefore $ Required equation of circumcircle is $ {{x}^{2}}+{{y}^{2}}=\frac{4{{a}^{2}}}{9}\Rightarrow 9{{x}^{2}}+9{{y}^{2}}=4{{a}^{2}} $