Q.
For a reaction, consider the plot of $logK$ versus $\frac{1}{ T}$ given in the figure.
If rate constant of this reaction at $\text{400 K is10}^{- 5}sec^{- 1}$ then the rate constant at $500K$ is :-
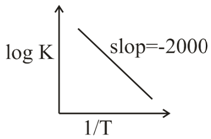
NTA AbhyasNTA Abhyas 2020
Solution:
