Q.
For a prism of prism angle $\theta=60^{\circ}$, the refractive indices of the left half and the right half are, respectively, $n _{1}$ and $n _{2}\left( n _{2} \geq n _{1}\right)$ as shown in the figure. The angle of incidence $i$ is chosen such that the incident light rays will have minimum deviation if $n _{1}= n _{2}= n =1.5$. For the case of unequal refractive indices, $n _{1}= n$ and $n _{2}=$ $n +\Delta n$ (where $\Delta n << n$ ), the angle of emergence $e=i+\Delta e$. Which of the following statement(s) is(are) correct?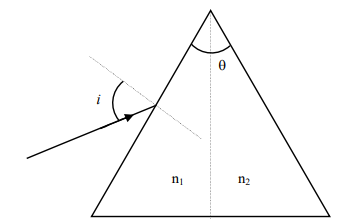
JEE AdvancedJEE Advanced 2021
Solution:
