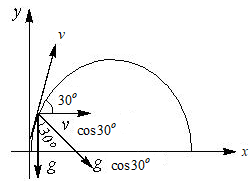
Question

For a particle projected from the ground with speed $u=20 \, ms^{- 1}$ at an angle of $60^\circ $ with horizontal. The radius of curvature of the path of the particle, when its velocity makes an angle of $30^\circ $ with horizontal will be.... $\left(\right.g \, =10 \, ms^{- 2}\left.\right)$ .

• A. 10.6 m
• B. 12.8 m
• C. 15.4 m
• D. 24.2 m

Answer 1

Answer: (C)

Let v be the velocity of particle when it makes $30^{\text{ο}}$ with horizontal

$v cos 30 = u cos 60$
$v \frac{\sqrt{3}}{2} = \left(20\right) \left(\frac{1}{2}\right)$
$v = \frac{\text{20}}{\sqrt{3}} ms^{- 1}$
now use centripetal acceleration $g cos 30^{\text{ο}}$
$mg cos 30^{\text{ο}} = \frac{\text{mv}^{2}}{\text{R}}$
$R = \frac{\left(\text{v}\right)^{2}}{g cos \left(\text{30}\right)^{\text{ο}}} = \frac{\left(\frac{\text{20}}{\sqrt{3}}\right)^{2}}{\text{10} \left(\frac{\sqrt{3}}{2}\right)}$
$= 15.4 m$