Question

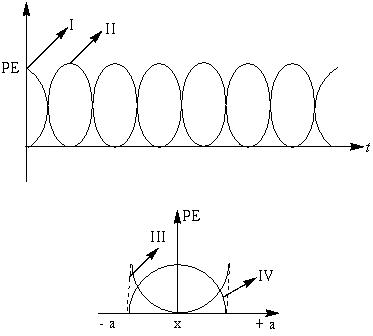
For a particle executing SHM, the displacement $x$ is given by $ \, x=Acos \omega t$ . Identify the graph which represents the variation of potential energy (PE) as a function of time $t$ and displacement $x$ .

• A. I, III
• B. II, IV
• C. II, III
• D. I, IV

Answer 1

Answer: (A)

Potential energy as a function of displacement :
$P E = \frac{1}{2} k y^{2}$
$\Rightarrow $ PE vs y graph will be an upwards parabola.
$\Rightarrow $ $\text{graph III}$
Potential energy as a function of time:
$P E = \frac{1}{2} k y^{2} = \frac{1}{2} k \left(\right. A \left(cos\right)^{2} \omega t \left.\right)^{2}$
$\Rightarrow P E = \frac{1}{2} k A^{2} \left(cos\right)^{2} \omega t = \frac{1}{2} k A^{2} \frac{\left(\right. 1 + cos 2 \omega t \left.\right)}{2}$
$\Rightarrow $ PE vs time is a cosine wave with angular frequency $2 \omega \Rightarrow g r a p h \text{ I} \text{.}$