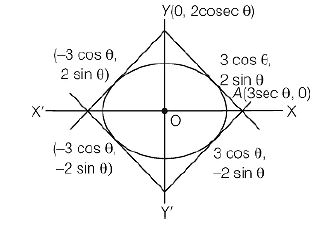
Question

For $0 <\, \theta <\, \frac{\pi}{2}$, four tangents are drawn at the four points $ \left(\pm3\,\cos\,\theta, \pm2\,\sin\,\theta\right)$ to the ellipse $ \frac{x^{2}}{9}+\frac{y^{2}}{4}=1$. If $A(\theta)$ denotes the area of the quadrilateral formed by these four tangents, th e minimum value of $A(\theta)$ is

• A. 21
• B. 24
• C. 27
• D. 30

Answer 1

Answer: (B)

We have,
Equation of ellipse
$\frac{x^{2}}{9}+\frac{y^{3}}{4}=1$

Equation of tangent at $(3\, \cos\theta, 2\sin\,\theta)$ is
$\frac{x}{3}\cos \theta +\frac{y}{2} \sin \theta =1$
Intercept of tangent is $(3\,\sec \, \theta, 0)$ and $(0, 2 \, cosec \, \theta)$
Area of quadrilateral
$=4 \times \frac{1}{2} 3\,\sec \theta \times 2\,cosec\, \theta$
$=12 \sec\theta\, cosec\,\theta =\frac{24}{\sin \, 2\theta}$
Minimum area $=24$