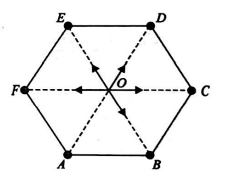
Q. Five point charges, each of value $+q$, are placed on five vertices of a regular hexagon of side $L$. The magnitude of the force on a point charge of value $-q$ coulomb placed at the center of the hexagon is
Electric Charges and Fields
Solution:
If there had been a sixth charge $+q$ at the remaining vertex of hexagon, force due to all the six charges on $-q$ at $O$ will be zero.
Now if $f$ is the force due to the sixth charge and $F$ due to the remaining five charges, then
$\vec{F}+\vec{f}=0, \text { i.e., } \vec{F}=-\vec{f}$
$|\vec{F}|=|\vec{f}|=\frac{1}{4 \pi \varepsilon_{0}} \frac{q \times q}{L^{2}}=\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{q}{L}\right)^{2}$