Q.
Five equal resistances each of value $R$ are connected to form a network as shown in figure. The equivalent resistance of the network between the points $A$ and $B$ is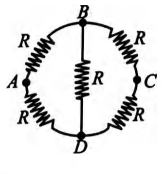
Current Electricity
Solution:
