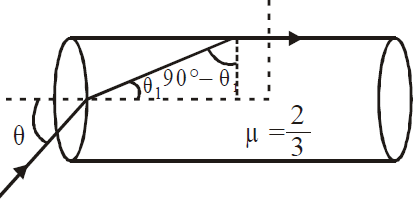
Q.
Find the value of $\theta$ in the given figure.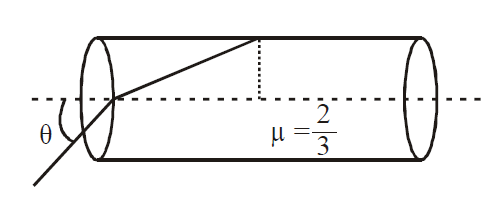
JIPMERJIPMER 2019
Solution:
For total internal reflection, $\mu$ $=\frac{1}{sin\,c}$
where, C = critical angle
Condition for TIR, the angle of incidence must be greater than critical angle C,
($90 - \theta_1) > C$
sin ($90 - \theta_1) > sin C$
$cos \theta_1$ $=\frac{1}{\mu}$
$cos \theta_1$ $ > \frac{1}{2/ \sqrt{3}}$
$cos \theta_1 > \frac{\sqrt{3}}{2}$
$\theta_1 > 30^{\circ}$
According to Snell’s law,
$\mu_1 sin \theta = \mu_{2} sin \theta_1$
$1 sin \theta =\frac{2}{\sqrt{3}} sin \theta_1$
$sin \theta =\frac{2}{\sqrt{3}} sin 30^{\circ}$
$sin \theta; =\frac{1}{\sqrt{3}}$
So,
$\theta; = sin^{-1} \left(\frac{1}{\sqrt{3}}\right)$