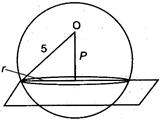
Q. Find the radius of the circle in which the sphere $ {{x}^{2}}+\text{ }{{y}^{2}}+\text{ }{{z}^{2}}+2x-2y-4z=19 $ is cut by the plane $ x+2y+2z+7=0 $ .
J & K CETJ & K CET 2014Three Dimensional Geometry
Solution:
Given equation of sphere is $ {{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2x-2y-4z-19=0 $ ?.(i) Its centre
$=(-1,1,2), $ radius
$=\sqrt{1+1+4+19} $
$=\sqrt{25}=5 $ and equation f plane is
$ x+2y+2z+7=0 $ ?.(ii) Length of the perpendicular from point $ (-1,\,1,\,2) $ to the plane (ii) is $ \left| \frac{-1+2+4+7}{\sqrt{1+4+4}} \right|=\frac{12}{3}=4 $
$ \therefore $ Radius of circle
$=\sqrt{{{(5)}^{2}}-{{(4)}^{2}}}=\sqrt{25-16}=3 $