Q.
Find the position of centre of mass of a uniform disc of radius $R$ from which a hole of radius $r$ is cut out. The centre of the hole is at a distance $R / 2$ from the centre of the disc.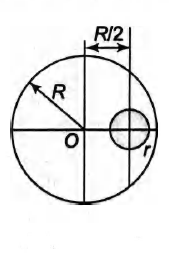
System of Particles and Rotational Motion
Solution: