Question

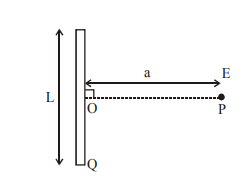
Find the electric field at point $P$ (as shown in figure) on the perpendicular bisector of a uniformly charged thin wire of length $L$ carrying a charge $Q$. The distance of the point $P$ from the centre of the rod is $a=\frac{\sqrt{3}}{2} L$

• A. $\frac{\sqrt{3} Q }{4 \pi \varepsilon_{0} L ^{2}}$
• B. $\frac{ Q }{3 \pi \varepsilon_{0} L ^{2}}$
• C. $\frac{ Q }{2 \sqrt{3} \pi \varepsilon_{0} L ^{2}}$
• D. $\frac{ Q }{4 \pi \varepsilon_{0} L ^{2}}$

Answer 1

Answer: (C)

$E =\frac{ k \lambda}{ a }\left(\sin \theta_{1}+\sin \theta_{2}\right)$
$E =\frac{1}{4 \pi \varepsilon_{0}} \times \frac{ Q }{ L } \times \frac{1}{\left(\frac{\sqrt{3} L }{2}\right)} \times(2 \sin \theta)$
$\tan \theta=\frac{ L / 2}{\frac{\sqrt{3} L }{2}}=\frac{1}{\sqrt{3}}$
$\sin \theta=\frac{1}{2}$
$E =\frac{1}{4 \pi \varepsilon_{0}} \times \frac{2 Q }{\sqrt{3} L ^{2}} \times\left(2 \times \frac{1}{2}\right)$
$E =\frac{ Q }{2 \sqrt{3} \pi \varepsilon_{0} L ^{2}}$