Q.
Find the centre of mass of a uniform $L$-shaped lamina (a thin flat plate) with dimensions as shown in the figure alongside. The mass of the lamina is $3\, kg$.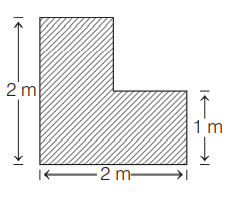
System of Particles and Rotational Motion
Solution:
