Question

Find the area bounded by the curves
$x^2+y^2=25$, $4y=|4-x^2|$ and x = 0 above the X-axis.

Answer 1

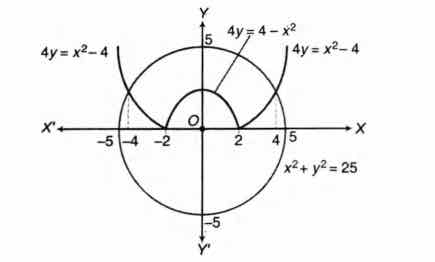
Given curves, $x^2+y^2=25$, $4y=|4-x^2|$ could be
sketched as below, whose points of intersection are
$x^2+\frac {(4-x^2)^2}{16}=25$
$\Rightarrow (x^2+24)$ $(x^2-16)$=0 &\Rightarrow & $x=\pm4$
$\therefore $ Required area=$2 \Big[ \int_0^4\sqrt{25-x^2} dx- \int_0^2 \Big( \frac {4-x^2}{4} \Big) dx- \int_2^4\Big( \frac {x^2-4}{4} \Big) dx \Big]$
=$2 \Big[ \Big[ \frac {x}{2} \sqrt{25-x^2} + \frac {25}{2} {sin}^{-1}{\frac {x}{5}}\Big]_0^4$
$-{\frac {1}{4}}\big[ 4x-\frac {x^3}{3}\big]_0^2-\frac {1}{4}\Big[ \frac {x^3}{3}-4x\Big]_2^4 \Big]$
$\Big[ \Big[ 6+\frac {25}{2} sin^{-1} \Big( \frac {4}{5}\Big)\Big]$-$\frac {1}{4} \Big[ 8-\frac {8}{3}\Big]$
$-{\frac {1}{4}}\Big[ \Big( \frac {64}{3}-16\Big)-\Big( \frac {8}{3}-8\Big)\Big]\Big]$
$=2\Big[6+\frac{25}{2} sin^{-1} \Big( \frac {4}{5}\Big)-\frac {4}{3}-\frac {4}{3}-\frac {4}{3}\Big]$
= $\Big[ 4+25 sin^{-1} \Big( \frac {4}{5}\Big)\Big]$ sq units