Q.
Figure shows two convex lenses $P$ and $Q$, each made up of three different transparent materials. The number of images formed of an object kept on the principal axis of lenses $P$ and $Q$ respectively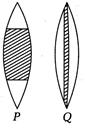
Jharkhand CECEJharkhand CECE 2015
Solution: