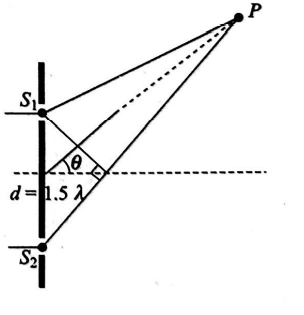
Question

Figure shows two coherent sources $S_{1}$ and $S_{2}$ emitting wavelength $\lambda$. The separation $S_{1} S_{2}=1.5 \lambda$ and $S_{1}$ is ahead in phase by $\pi / 2$ relative to $S_{2}$. Then the maxima occur in direction $\theta$ given by $\sin ^{-1}$ of
(i) $ 0 $
(ii) $ 1 / 2$
(iii) $-1 / 6 $
(iv) $-5 / 6$
Correct options are

• A. (ii), (iii), and (iv)
• B. (i), (ii), and (iii)
• C. (i), (iii), and (iv)
• D. All the above

Answer 1

Answer: (A)

$\delta=$ phase difference between the waves from $S_{1}$ and $S_{2}$ at
$P=\frac{\pi}{2}-\frac{2 \pi}{2}(d \sin \theta)$
For maximum intensity at $P, \delta=n \pi$, where $n=0, \pm 1$, $\pm 2, \ldots$
$\therefore \frac{2 \pi}{2}(1.5 \lambda \sin \theta) \frac{\pi}{2}=n \pi$
$\Rightarrow n-\frac{1}{2}=3 \sin \theta$
$\Rightarrow \sin \theta=\left(\frac{n-\frac{1}{2}}{3}\right)$
For $n=0, \sin \theta=-\frac{1}{6}$
For $n=\pm 1, \sin \theta=\frac{1}{6},-\frac{1}{2}$
For $n=\pm 2, \sin \theta=\frac{1}{2},-\frac{5}{6}$