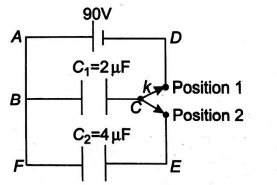
Question

Figure shows two capacitors of capacitance $2\, \mu F$ and $4 \,\mu F$ and a cell of $90\, V$. The switch $k$ is such that when it is in position $1$ , the circuit $A B C D$ is closed and when it is in position $2$, the circuit $B C E F$ is closed. The resistance of both the circuits is negligible so that the capacitor gets fully charged instantly. Initially, the switch is in position $1$. Then it is turned in position $2$. This makes one cycle. It is then again turned in position $1$ and then in position $2$. Now two cycles are completed. Find the charge (in $\times 10^{2} \mu C$ ) on the capacitor of capacitance $4 \,\mu F$ after two cycles.

Answer 1

Initially when key $k$ is in position $1$ , charge on $C_{1}$ is
$Q_{1}=180 \,\mu C$

As the key is pushed to position $2, C_{1}$ and $C_{2}$ are in parallel
$\therefore$ Charge on $C_{2}$ is $q_{2}=C_{2}\left(\frac{\text { net charge on } C_{1} \& C_{2}}{C_{1}+C_{2}}\right)$
$=4 \times \frac{180}{6}=120\, \mu C$
Again when key $k$ is pushed position $1$ , charge on $C_{1}$ is
$Q_{1}=180\, \mu C$
As the key is again pushed to position $2$, charge on
$\therefore $ Charge on $ C_{2} $ is $ q_{2} =C_{2}\left(\frac{\text { net charge on } C_{1} \& C_{2}}{C_{1}+C_{2}}\right) $
$=4 \times \frac{180+120}{6}=200\, \mu C$