Question

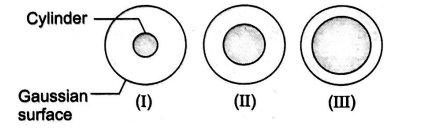
Figure shows, in cross section, three solid cylinders, each of length $L$ and uniform charge $Q$. Concentric with each cylinder is a cylindrical Gaussian surface, with all three surfaces having the same radius. Rank the Gaussian surfaces according to the electric field at any point on the surface, greatest first.

• A. I $\rightarrow$ II $\rightarrow$ III
• B. II $\rightarrow$ I $\rightarrow$ III
• C. III $\rightarrow$ II $\rightarrow$ I
• D. all tie

Answer 1

Answer: (D)

In each case: $\oint \vec{E} \cdot d \vec{A}=\frac{q_{\text { enclosed} }}{\varepsilon_{0}}$
$E \oint d A=\frac{Q}{\varepsilon_{0}} $
$ E\left(4 \pi r^{2}\right)=\frac{Q}{\varepsilon_{0}}$
$ E$ $ = \frac {1}{4\pi \varepsilon_{0}}\frac{Q}{r^{2}} $
As charged enclosed within the Gaussian surface is the same, the radius of Gaussian surface is equal. Hence, the magnitude of electric field will be equal.