Q.
Figure shows a system consisting of a massless pulley, a spring of force constant $k$ and a block of mass $m$. If the block is slightly displaced vertically down from its equilibrium position and then released, the period of its vertical oscillation is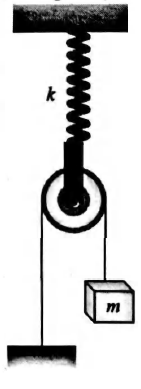
Oscillations
Solution:
