1. Tardigrade
  2. Question
  3. Physics
  4. Figure shows a projectile thrown with speed u=20 m / s at an angle 30° with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

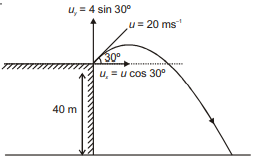
Q. Figure shows a projectile thrown with speed $u=20\, m / s$ at an angle $30^{\circ}$ with horizontal from the top of a building $40 m$ high. Then the horizontal range of projectile isPhysics Question Image

Motion in a Plane

Solution:

$S_{y}=u_{y} T+\frac{1}{2} g_{y} T^{2}$
$-40=4 \sin 30 T-\frac{1}{2} g T^{2}$
$-40=20 \times \frac{1}{2} T-5 T^{2}$
$-8=2 T-T^{2}$
$T^{2}-2 T-8=0$
$T^{2}-4 T+2 T-8=0$
$T=-2,4$
$R=u \cos \theta T=20 \times \frac{\sqrt{3}}{2} \times 4$
$R=40 \sqrt{3} m$

Solution Image