Q.
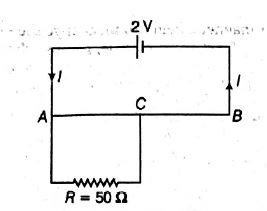
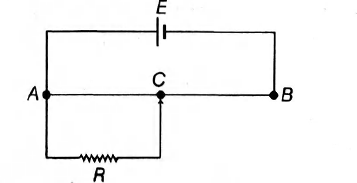
Figure shows a potentiometer. Length of the potentiometer wire $ AB $ is $ 100 \,cm $ and its resistance is $ 100\, \Omega $ . $ EMF $ of the battery $ E $ is $ 2 V $ . A resistance $ R $ of $ 50 \Omega $ draws current from the potentiometer. What is the voltage across $ R $ when the sliding contact $ C $ is at the mid-point of $ AB $ ?
AMUAMU 2018Current Electricity
Solution: