Q.
Figure shows a counterweight of mass $m$ suspended by a cord wound around a spool of radius $r$, forming part of a turntable supporting the object. The turntable can rotate without friction. When the counterweight is released from rest, it descends through a distance $h$, acquiring a speed $v$. The moment of inertia $I$ of the rotating apparatus is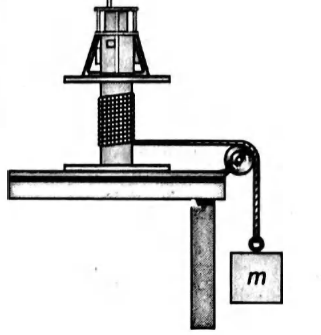
System of Particles and Rotational Motion
Solution: