Q.
Figure shows a conducting loop consisting of a half-circle of radius $r = 0.20\,m$ and three straight sections. The half-circle lies in a uniform magnetic field $B$ that is directed out of the page, the field magnitude is given by $ B=(4.0\,T/s^{2})t^{2}+(2.0\,T/s)t+3.0\,T $ An ideal battery with $ \varepsilon_{0}=2.0\,V $ is connected to the loop. The resistance of the loop is $ 2.0\,\Omega $ . The current in the loop at $ t=10\,s $ will be close to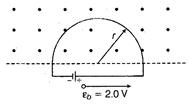
AMUAMU 2013
Solution: