Question

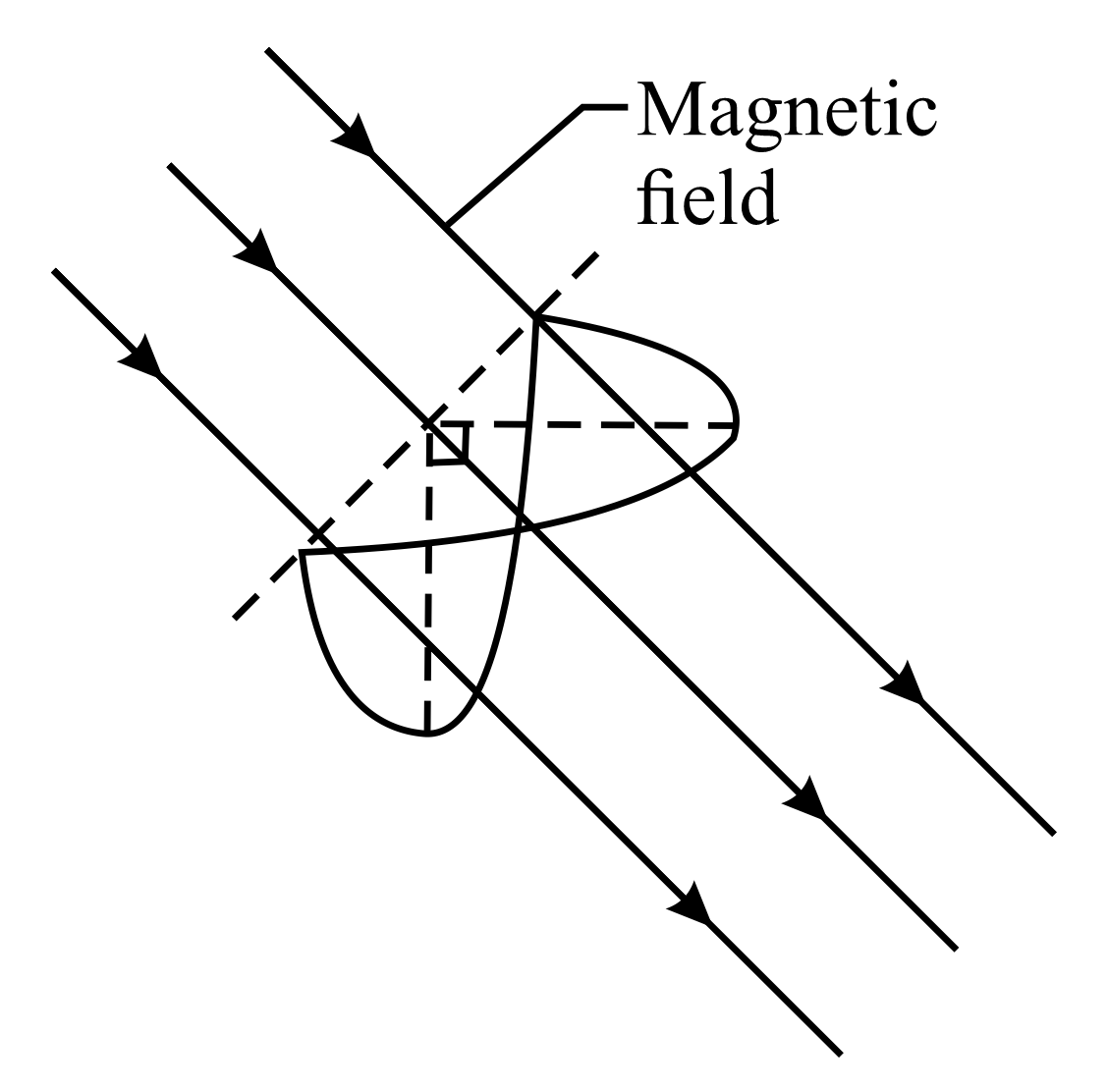
Figure shows a closed loop of wire that consists of a pair of equal semicircles, of radius $R$ , lying in mutually perpendicular planes. The loop was formed by folding a flat circular loop along a diameter until the two halves became perpendicular to each other. A uniform magnetic field of magnitude $B$ is directed perpendicular to the fold diameter and makes equal angles $\left(\right.$ of $45^\circ \left.$ with the planes of the semicircles, initially $\left(\right.t=0\left.\right)$ . The loop is rotated at a constant angular velocity $\omega $ about the fold diameter. This induces an emf, which causes a current to flow in the wire. The resistance per unit length of the wire is $\lambda $ . The magnetic moment of the loop is

• A. $\left(\frac{B \pi R^{3} \omega }{2 \sqrt{2} \lambda } sin \omega t\right)$
• B. $\left(\frac{B \pi R^{3} \omega }{2 \lambda } cos \omega t\right)$
• C. $\left(\frac{B \pi R^{3} \omega }{4 \lambda } cos \omega t\right)$
• D. $\left(\frac{B \pi R^{3} \omega }{4 \lambda } sin \omega t\right)$

Answer 1

Answer: (D)

The flux of the magnetic field through the loop when it has rotated through $\theta =\omega t$ , is
$\Phi=\frac{B \pi R^{2}}{2}\left(2 cos 45 ^\circ cos \omega t\right)$
$EMF=-\frac{d \Phi}{d t}=\frac{B \pi R^{2} \omega }{\sqrt{2}}sin\omega t$
Current, $i=\frac{E M F}{\lambda . 2 \pi R}$
Magnetic moment $=$ current $\times $ area $=\left(\frac{B \pi R^{3} \omega }{4 \lambda } sin \omega t\right)$