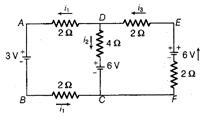
Q.
Figure shows a circuit with three ideal batteries in it. The circuit elements have the following values $\Delta V_{B_{1}}=3.0 \,V , \Delta V_{B_{2}}=6.0\, V \,R_{1}=2.0 \,\Omega, R_{2}=4.0\, \Omega$ The currents $i_{1}, i_{2}$ and $i_{3}$ as shown in the circuit have the values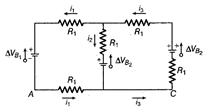
AMUAMU 2013Current Electricity
Solution:
Given circuit
In $A B C D$, From Kirchhoffs law
$2 i_{1}+2 i_{1}-4 i_{2}+3-6=0$
$4 i_{1}-4 i_{2}=3 \ldots$ (i)
and in $C D E F$ From Kirchhoffs law
$2 i_{3}+4 i_{2}+6-6+2 i_{3}=0$
$4 i_{2}+4 i_{3}=0 i_{2}=-i_{3}$ .. (ii)
$i_{1}+i_{2}=i_{3} \ldots$ (iii)
From Eq. (ii), we get
$i_{1}+i_{2}=-i_{2}$
From Eq. (i), $i_{1}=-2 i_{2} $
$3=4\left(-2 i_{2}\right)-4 i_{i}$
$ 3=-12 i_{2}$
$i_{2}=-0.25\, A$
$ i_{1}=-2 i_{2}=0.50 \,A$
and $i_{3}=-i_{2}=0.25 \,A$