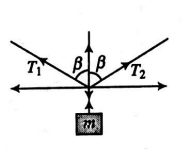
Q.
Figure represents a light inextensible string $A B C D E$ in which $A B=B C=C D=D E$ and to which are attached masses $M, m$, and $M$ at the points $B, C$, and $D$, respectively.
The system hangs freely in equilibrium with ends $A$ and $E$ of the string fixed in the same horizontal line. It is given that $\tan \alpha=3 / 4$ and $\tan \beta=12 / 5$. Then the tension in the string $B C$ is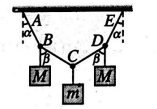
Laws of Motion
Solution:
$\tan \beta=\frac{12}{5}$
$\therefore \cos \beta=\frac{5}{13}$
$T_{1} \cos \beta+T_{2} \cos \beta=m g$ ...(i)
$T_{1} \sin \beta=T_{2} \sin \beta$ ...(ii)
$\therefore T_{1}=T_{2}=T$
$\therefore 2 T \cos \beta=m g$
$\Rightarrow T=\frac{m g}{2 \cos \beta}$
$\Rightarrow T=\frac{13}{10} m g$