Question

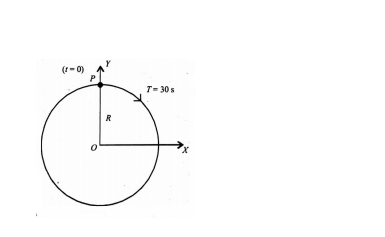
Figure depicts a circular motion of the particle $P$. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHM motion of the $x$ -projection of the radius vector of the rotating particle $P$

• A. $R\, \sin \left[\frac{\pi}{2}-\frac{\pi}{15} t\right]$
• B. $R \sin \left[\frac{\pi}{15} t-\frac{\pi}{2}\right]$
• C. $R\, \cos \left[\pi-\frac{\pi}{15} t\right]$
• D. $R\, \cos \left[\frac{\pi}{15} t-\frac{\pi}{2}\right]$

Answer 1

Answer: (D)

In this case, at $t=0,$ OP makes an angle of $90^{\circ}$
or $\frac{\pi}{2}$ with the $x$ -axis. After a time $t,$ it covers an angle
$\frac{2 \pi}{T} t$ in the clockwise sense and makes an angle of
$\left(\frac{\pi}{2}-\frac{2 \pi t}{T}\right)$ with the $x$ -axis. The projection $OP$ on the $x$
axis at time $t$ is given by $x(t)=R \cos \left[\frac{\pi}{2}-\frac{2 \pi t}{T}\right]$
For $T=30 \,s , x(t)=R \cos \left[\frac{\pi}{2}-\frac{\pi}{15} t\right]$
$=R \cos \left[\frac{\pi t}{15}-\frac{\pi}{2}\right]$
as $\cos (-\theta)=\cos \,\theta$