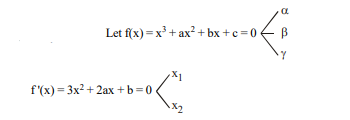Q.
$ f ( x )=0$ is a cubic equation with positive and distinct roots $\alpha, \beta, \gamma$ such that $\beta$ is harmonic mean between the roots of $f ^{\prime}( x )=0$. If $r =\left[\frac{2 \beta}{\alpha+\gamma}\right]+\left[\frac{2 \alpha \gamma}{\alpha \beta+\beta \gamma}\right]$, then the value of $\displaystyle\sum_{ i =1}^3( i )^{ r }$ is
$[$ Note $:[k]$ denotes greatest integer function less than or equal to $k$. $]$
Sequences and Series
Solution: