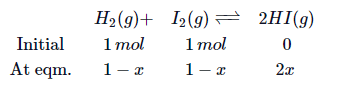Question

Equimolar concentrations of $H_2$ and $I_2$ are heated to equilibrium in a $2$ litres flask. At equilibrium, the forward and the backward rate constants are found to be equal. What percentage of initial concentration of $H_2$ has reacted at equilibrium ?

• A. 33%
• B. 66%
• C. 50%
• D. 40%

Answer 1

Answer: (A)

Molar conc $\frac{1-x}{2} \,\,\frac{1-x}{2}\,\,\frac{2x}{2}mol\,L^{-1}$
$K=\frac{\left(2x\right)^{2}}{\left(1-x\right)\left(1-x\right)}=\frac{4x^{2}}{\left(1-x\right)^{2}}$
But $K_{f} k=1\Rightarrow K=1$
$\therefore \frac{2x}{1-x}=1$ or $x=1/ 3$
Percent dissociation $=100/3=33.33\%$