Question

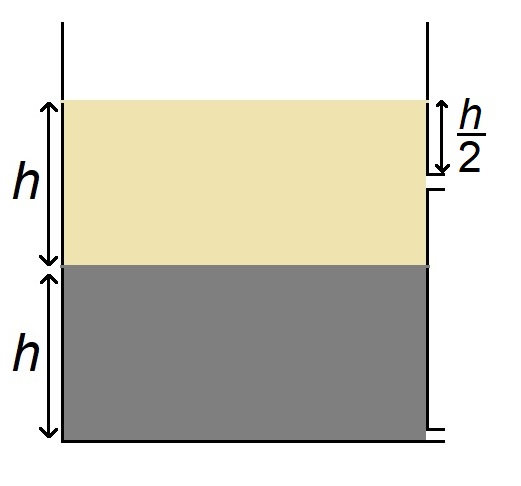
Equal volumes of two immiscible liquids of density $2\rho $ and $4\rho $ , respectively, are filled in the vessel as shown in the figure. Two small holes are punched at depth $\frac{h}{2}$ and $2h$ , respectively, from the surface of the lighter liquid. If $v_{1}$ and $v_{2}$ are the velocities of efflux at these holes, then the ratio of $\frac{v_{1}}{v_{2 \, }}$ is

• A. $1/3$
• B. $1/\sqrt{3}$
• C. $1/2$
• D. $1/\sqrt{2}$

Answer 1

Answer: (B)

$2\rho g\frac{h}{2}=\frac{1}{2}2\rho v_{1}^{2} \, \, \, \Rightarrow \, \, \, v_{1}=\sqrt{g h}$
$4\rho gh+2\rho gh=\frac{1}{2}\cdot 4\rho v_{2}^{2}$
$\Rightarrow 6\rho gh=2\rho v_{2}^{2} \, \, \, \Rightarrow \, \, \, v_{2}=\sqrt{3 g h}$
$\therefore \frac{v_{1}}{v_{2}}=\frac{1}{\sqrt{3}}$