Q.
Electric field at centre O of semicircle of radius a having linear charge density $\lambda$ given as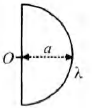
AIPMTAIPMT 2000Electrostatic Potential and Capacitance
Solution:
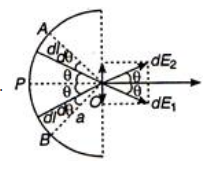
Considering symmetric elements each of length $dl$ at A and B, we note that electric fields perpendicular to PO are cancelled and those along PO are added. The electric field due to an element of length $dl(=ad\theta )$ along PO.
$dE=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{dq}{{{a}^{2}}}\cos \theta $
$(\because dl=ad\theta )$
$=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{\lambda dl}{{{a}^{2}}}\cos \theta$
$=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{\lambda (ad\theta )}{{{a}^{2}}}\cos \theta$ Net electric field at O
$E=\int_{-\pi /2}^{\pi /2}{dE=2\int_{O}^{\pi /2}{\frac{1}{4\pi {{\varepsilon }_{0}}}}}\frac{\lambda a\cos \theta \,d\theta }{{{a}^{2}}}$
$=2\cdot \frac{1}{4\pi {{\varepsilon }_{O}}}\frac{\lambda }{a}[\sin \theta ]_{o}^{\pi /2}$
$=2\cdot \frac{1}{4\pi {{\varepsilon }_{O}}}\cdot \frac{\lambda }{a}\cdot 1=\frac{\lambda }{2\pi {{\varepsilon }_{o}}a}$