Question

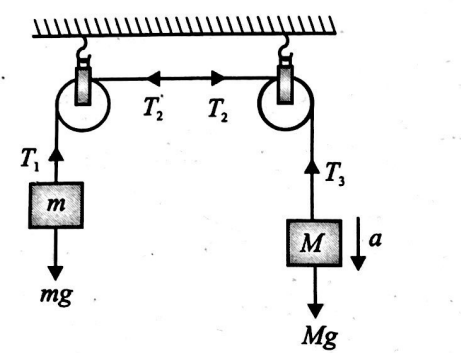
Each pulley in the figure has radius $r$ and moment of inertia $I$. The acceleration of the block is

• A. $\frac{(M-m) g}{\left(M+m+\frac{2 I}{r^{2}}\right)}$
• B. $\frac{(M-m) g}{\left(M+m-\frac{2 I}{r^{2}}\right)}$
• C. $\frac{(M-m) g}{\left(M+m+\frac{I}{r^{2}}\right)}$
• D. $\frac{(M-m) g}{\left(M+m-\frac{I}{r^{2}}\right)}$

Answer 1

Answer: (A)

$T_{1}-m g=m a\,\,\,...(i)$
$r\left(T_{2}-T_{2}\right)=I \alpha\,\,\,...(ii)$
$M g-T_{3}=M a\,\,\,...(iii)$
$r\left(T_{3}-T_{2}\right)=I \alpha\,\,\,...(iv)$
and $a=R \alpha$
From Eqs. (ii) and (iv), we get
$T_{3}-T_{1}=\frac{2 I a}{R^{2}}$
From Eqs. (i) and (iii), we get
$(M-m) g=(M+m) a+T_{3}-T_{1}$
$(M-m) g=(M-m) a+\frac{2 I a}{r^{2}}$
$\Rightarrow a=\frac{(M-m) g}{\left(M+m+\frac{2 I}{r^{2}}\right)}$