Question

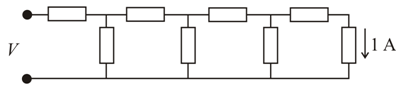
Each element in the finite chain of resistors shown in the figure is $1\,\Omega.$ A current of $1\,A$ flows through the final element. The potential difference $V$ across the input terminals of the chain is $\left(30 + n\right)$ volt. Find $n$

Answer 1

Number the resistors, starting with the last element in the chain. As current of $1A$ flows through the first resistor, a current of $1A$ has to flow through the second one as well, thus there is a potential different $\left(p . d\right)$ of $1V$ across each resistor. As a consequence, the $p.d.$ across the third resistor is $\left(1 + 1\right)=2V,$ and the current flowing through it must be $2A$ . The current flowing through the next resistor is $\left(1 + 2\right)$ $=3A.$ The current in the fifth resistor can be determined using the $p.d.$ $\left(2 + 3\right)=5V$ across the resistors with currents of $2$ and $3A$ , respectively, flowing through them and so on, as shown in figure.