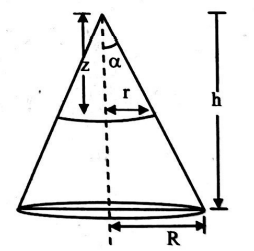
Question

Distance of the centre of mass of a solid uniform cone from its vertex is $z _{0}$. If the radius of its base is $R$ and its height is $12\, cm$ then $z_{0}$ is equal to _______$cm$.

Answer 1

$dm =\rho \pi r ^{2} dz$
From figure,
$\tan \alpha=\frac{ r }{ z }=\frac{ R }{ h }$
$\therefore r =\frac{ R }{ h } Z$
Now, $z_{C M}=\frac{\int z d m}{\int d m}=\frac{\int\limits_{0}^{h} \rho \pi r^{2} z d z}{\frac{1}{3} \pi R^{2} h \rho}$
$=\frac{3}{ R ^{2} h } \int\limits_{0}^{ h }\left(\frac{ R }{ h } z \right)^{2} zdz $
$=\frac{3}{ hR ^{2}}\left(\frac{ R ^{2}}{ h ^{2}}\right) \int\limits_{0}^{ h } z ^{3} dz$
$=\frac{3}{ h ^{3}}\left[\frac{ z ^{4}}{4}\right]_{0}^{ h }=\frac{3 h }{4}$
$=\frac{3 \times 12}{4}=9\, cm$