Question

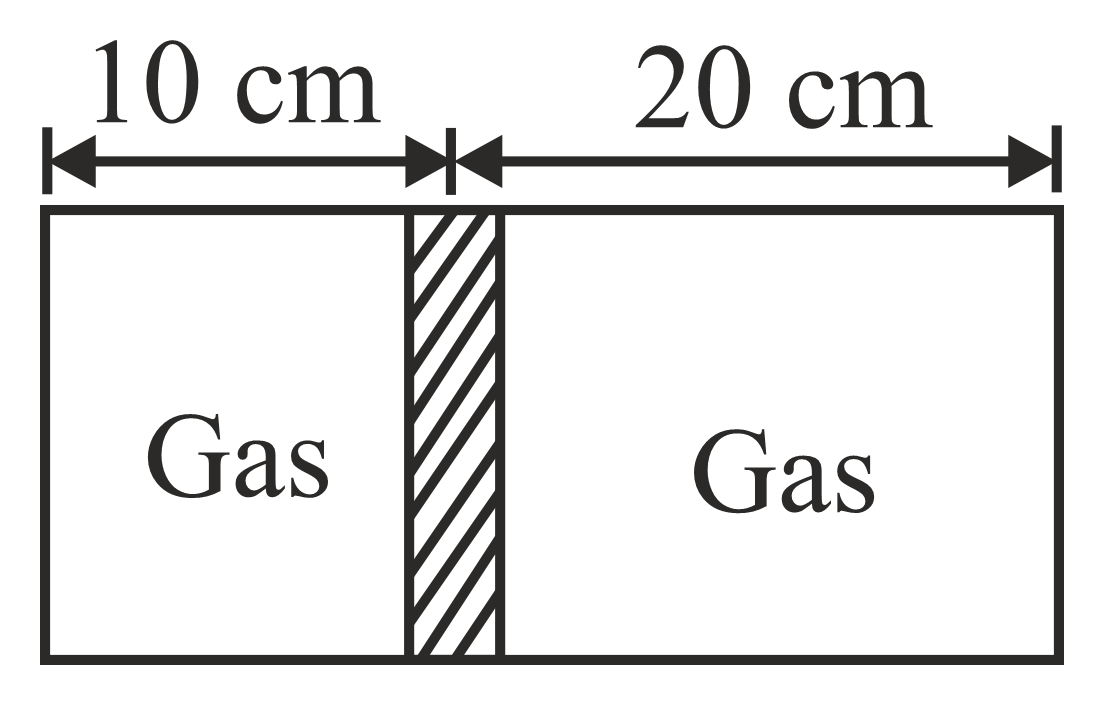
Diagram shows a horizontal cylindrical container of length $30cm$ , which is partitioned by a tight-fitting separator. The separator is diathermic but conducts heat very slowly. Initially the separator is in the state shown in the diagram. The temperature of left part of cylinder is $100K$ and that on right part is $400K$ . Initially the separator is in equilibrium. As heat is conducted from right to left part, separator displaces to the right. Find the displacement of separator after a long when gases on the two parts of cylinder are in thermal equilibrium.

Answer 1

It is given that initially the separator is in equilibrium; thus pressure on both sides of the gas is equal say, it is P_i. If $A$ be the area of cross-section of cylinder, number of moles of gas in left and right part, $
n _{1}=\frac{ P _{ i }(10 A )}{ R (100)}
$
and $ n _{2}=\frac{ P _{ i }(20 A )}{ R (400)}$
Finally, if separator is displaced to right by a distance $x$, we have
$
n_{1}=\frac{P_{f}(10+x) A}{R T_{f}}
$
and $ n_{2}=\frac{P_{f}(20-x) A}{R T_{f}}$
Here $P _{f}$ and $T _{f}$ are the final pressure and temperature on both sides after a long time.
Now if we equate the ratio of moles in initial and final states, we get
$
\frac{n_{1}}{n_{2}}=\frac{(10 A / 100)}{(20 A / 400)}=\frac{(10+x) A}{(20-x) A}
$
$
2(20-x)=10+x
$
$
x =10 cm
$