Question

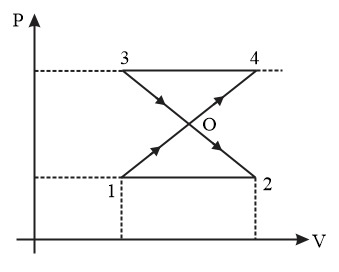
Determine the work done by an ideal gas undergoing a cyclic process from $1 \rightarrow 4 \rightarrow 3 \rightarrow 2 \rightarrow 1$ . Given $P_{1}=10^{5} \, Pa, \, P_{0} \, = \, 3\times 10^{5} \, Pa, \, P_{3}=4\times 10^{5} \, Pa$ and $V_{2}-V_{1}=10 \, L$ .

• A. $740J$
• B. $750 \, J$
• C. $730 \, J$
• D. $745 \, J$

Answer 1

Answer: (B)

From figure
$\frac{\text{V}_{4} - \text{V}_{3}}{\text{V}_{2} - \text{V}_{1}} = \frac{\text{P}_{3} - \text{P}_{0}}{\text{P}_{0} - \text{P}_{1}} \Rightarrow \frac{\text{V}_{4} - \text{V}_{3}}{1 0} = \frac{4 \times 1 0^{5} - 3 \times 1 0^{5}}{3 \times 1 0^{5} - 1 0^{5}}$
$V_{4}-V_{3}=5L$
Now, work done
$\text{W} = \left(\frac{1}{2} \times 1 \times 2 \times 1 0^{5} - \frac{1}{2} \times 5 \times 1 \times 1 0^{5}\right) \times 1 0^{- 3} = 7 5 0 J$