Question

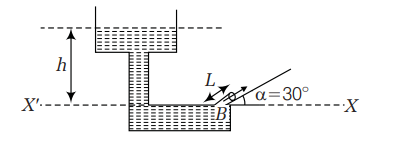
Determine the height above the dashed line $X X^{\prime}$ attained by the water stream coming out through the hole is situated at point $B$ in the diagram given below. Given that $h=10\, m , L=2\, m$ and $d=30^{\circ}$.

• A. 10 m
• B. 7.1 m
• C. 5 m
• D. 3.2 m

Answer 1

Answer: (D)

Let the velocity at point $B$ is $v_{B}$.
From conservation of total mechanical energy,
$m g[h-L \sin \alpha] =\frac{1}{2} m v_{B}^{2} $
$\Rightarrow v_{B}^{2} =2 g(h-L \sin \alpha)$
$=2 g\left(10-2 \times \frac{1}{2}\right)$
$\Rightarrow v_{B}^{2} =18\, g$
Now, let maximum height attained by water stream, be $(H)$.
$\therefore H =L \sin \theta+\frac{V_{B}^{2} \sin ^{2} \alpha}{2 g} $
$\Rightarrow H =2 \times \frac{1}{2}+\frac{18 g\left(\frac{1}{2}\right)^{2}}{2 g} $
$=1+\frac{18}{8}=3.25\, m$