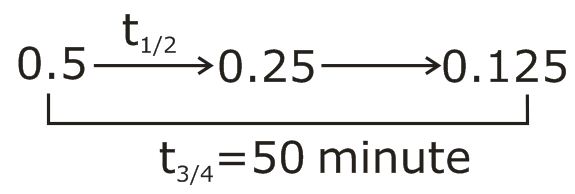Question

Decomposition of $H_{2}O_{2}$ follows a first order reaction. In fifty minutes the concentration of $\text{H}_{2} \text{O}_{2}$ decreases from $0.5$ to $0.125 \, M$ in one such decomposition. When the concentration of $H_{2}O_{2}$ reaches $0.05 \, M$ , the rate of formation of $O_{2}$ will be:

• A. $2.66 \, Lmin^{- 1} \, a t \, S T P$
• B. $1.34\times 10^{- 2} \, mol \, m i n^{- 1}$
• C. $6.93\times 10^{- 2} \, mol \, m i n^{- 1}$
• D. $6.93\times 10^{- 4} \, mol \, m i n^{- 1}$

Answer 1

Answer: (D)

$\text{H}_{\text{2}} \text{O}_{\text{2}} \rightarrow \text{H}_{\text{2}} \text{O} + \frac{1}{2} \text{O}_{\text{2}}$

$-\frac{d \left[\right. H_{2} O_{2} \left]\right.}{dt}=\frac{d\left[\right.H_{2}O\left]\right.}{dt}=2\frac{d\left[\right.O_{2}\left]\right.}{dt}$



$t_{\frac{1}{2}}=25$

$\text{t}_{\frac{\text{1}}{\text{2}}} \text{=} \frac{\text{0} \text{.69314}}{\text{k}}$

$\text{k} \, \text{=} \, \frac{\text{0} \text{.69314}}{\text{25}}$

rate of reaction = $k\left[\right.H_{2}O_{2}\left]\right.$

$\therefore \, \frac{d \left[\right. O_{2} \left]\right.}{dt}=\frac{1}{2}\times k\left[\right.H_{2}O_{2}\left]\right.$

$=\frac{1}{2}\times \frac{0.69314}{25}\times 0.05$

$=6.93\times 10^{- 4} \, mol \, m i n^{- 1}$