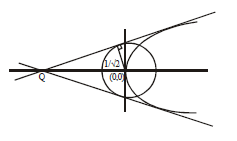
Q. Consider two straight lines, each of which is tangent to both the circle $x^2 + y^2 = \frac{1}{2}$ and the parabola $y^2 = 4x$. Let these lines intersect at the point $Q$. Consider the ellipse whose center is at the origin $O(0,0)$ and whose semi-major axis is $OQ$. If the length of the minor axis of this ellipse is $\sqrt{2}$ , then which of the following statement(s) is (are) TRUE?
JEE AdvancedJEE Advanced 2018
Solution:
Let equation of common tangent is $y = mx + \frac{1}{m}$
$\therefore \left|\frac{0+0+\frac{1}{m}}{\sqrt{1+m^{2}}} \right| = \frac{1}{\sqrt{2}} \Rightarrow m^{4} + m^{2} - 2 = 0 \Rightarrow m = \pm1$
Equation of common tangents are y = x + 1 and y = -x - 1 point Q is (-1, 0)
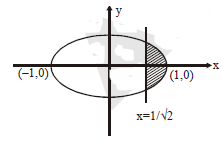
$\therefore $ Equation of ellipse is $ \frac{x^{2}}{1} + \frac{y^{2}}{1/2} = 1 $
(A) $e = \sqrt{- \frac{1}{2}} = \frac{1}{\sqrt{2}} LR = \frac{2b^{2}}{a} = 1 $
(C) .....
Area 2 . $\int^{1}_{1/\sqrt{2}} \frac{1}{\sqrt{2}}. \sqrt{1-x^{2}} dx =\sqrt{2}\left[\frac{x}{2} \sqrt{1-x^{2}} + \frac{1}{2} \sin^{-1}x \right]^{1}_{1/\sqrt{2}} $
$= \sqrt{2} \left[\frac{\pi}{4} - \left(\frac{1}{4} + \frac{\pi}{8}\right)\right]=\sqrt{2} \left(\frac{\pi}{8} - \frac{1}{4}\right) = \frac{\pi-2}{4\sqrt{2}} $
correct answer are (A) and (D)