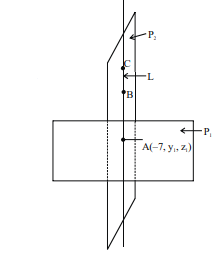
Q. Consider two planes $P_1: 2 x-3 y+z=-5$ and $P_2: x-4 y-14 z=5$. If a line $L$ which is perpendicular to line of intersection of planes $P_1 \& P_2$ and whose one point $A\left(-7, y_1, z_1\right)$ lies on the plane $P_1$ and points $B\left(x_2, y_2, z_2\right)$ and $C\left(x_3, y_3, z_3\right)$ lie on plane $P_2$ has the equation $\frac{x+7}{a}=\frac{y-y_1}{-b}$ $=\frac{ z - z _{ I }}{ c }$, where $a , b , c \in N$, then
Vector Algebra
Solution: