Q. Consider two particles of equal mass $m$ . If one particle is stationary while the other collides with this particle obliquely with velocity $v$ . Now, what is the angle between the velocity vectors of the two particles after the collision?
NTA AbhyasNTA Abhyas 2022
Solution:
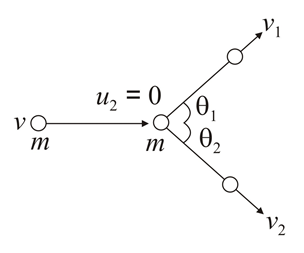
Given that mass of each particle $=m$
initial velocity of one moving particle $=v$
initial velocity of other particle $=0$ (because it is stationary)
Let after collision,
One particle moves with velocity $v_{1}$ with angle $\theta _{1}$ w.r.t. $x-$ axis,
and other particle moves with velocity $v_{2}$ with angel $\theta _{2}$ w.r.t. $x-$ axis.
Now, by momentum conservation in $x-$ direction
(initial momentum) along $x-$ axis. = (final momentum) along $y-$ axis
$\left(\right.p_{i}\left(\left.\right)_{x - a x i s}=\left(\right.p_{f}\left(\left.\right)_{x - a x i s}$
$\Rightarrow mv+m\left(\right.0\left.\right)=mv_{1}cos\left(\theta \right)_{1}+mv_{2}cos\left(\theta \right)_{2}$
$\Rightarrow v=v_{1}cos\left(\theta \right)_{1}+v_{2}cos\left(\theta \right)_{2}...\left(\right.1\left.\right)$
Now, by momentum conservation in $y-$ direction
$\left(\right.p_{i}\left(\left.\right)_{y - a x i s}=\left(\right.p_{f}\left(\left.\right)_{y - a x i s}$
$\Rightarrow m\left(\right.0\left.\right)+m\left(\right.0\left.\right)=mv_{1}sin\left(\theta \right)_{1}-mv_{2}sin\left(\theta \right)_{2}$
$\Rightarrow 0=v_{1}sin\left(\theta \right)_{1}-v_{2}sin\left(\theta \right)_{2}...\left(\right.2\left.\right)$
and by law of conservation of kinetic energy
$\left(\right.Kineticenergy\left(\left.\right)_{b e f o r e c o l l i s i o n}=\left(\right.Kineticenergy\left(\left.\right)_{a f t e r c o l l i s i o n}$
$\Rightarrow \frac{1}{2}mv^{2}+\frac{1}{2}m\left(\right.0\left(\left.\right)^{2}=\frac{1}{2}mv_{1}^{2}+\frac{1}{2}mv_{2}^{2}$
$\Rightarrow v^{2}=v_{1}^{2}+v_{2}^{2}...\left(\right.3\left.\right)$
Addition of square of eq. (1) and eq. (2)
$\Rightarrow v^{2}+0^{2}=\left(\right.v_{1}cos\left(\theta \right)_{1}+v_{2}cos\left(\theta \right)_{2}\left(\left.\right)^{2}+\left(\right.v_{1}sin\left(\theta \right)_{1}-v_{2}sin\left(\theta \right)_{2}\left(\left.\right)^{2}$
$\Rightarrow v^{2}=v_{1}^{2}cos\theta _{1}^{2}+v_{2}^{2}cos\theta _{2}^{2}+2v_{1}v_{2}cos\theta _{1}cos\theta _{2}$ $+v_{1}^{2}sin\theta _{1}^{2}+v_{2}^{2}sin\theta _{2}^{2}-2v_{1}v_{2}sin\theta _{1}sin\theta _{2}$
$\Rightarrow v^{2}=v_{1}^{2}\left(\right.cos\theta _{1}^{2}+sin\theta _{2}^{2}\left.\right)+v_{2}^{2}\left(\right.cos\theta _{2}^{2}+sin\theta _{2}^{2}\left.\right)$
$2v_{1}v_{2}\left(\right.cos\left(\theta \right)_{1}cos\left(\theta \right)_{2}-sin\left(\theta \right)_{2}sin\left(\theta \right)_{2}\left.\right)$
$\Rightarrow v^{2}=v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}\left(\right.cos\left(\theta \right)_{1}cos\left(\theta \right)_{2}-sin\left(\theta \right)_{1}sin\left(\theta \right)_{2}\left.\right)$
Using eq. (3)
$\Rightarrow v_{1}^{2}+v_{2}^{2}=v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}\left(\right.cos\left(\theta \right)_{1}cos\left(\theta \right)_{2}-sin\left(\theta \right)_{1}sin\left(\theta \right)_{2}\left.\right)$
$\Rightarrow 2v_{1}v_{2}cos\left(\right.\left(\theta \right)_{1}+\left(\theta \right)_{2}\left.\right)=0$
$\Rightarrow cos\left(\right.\left(\theta \right)_{1}+\left(\theta \right)_{2}\left.\right)=0$
$\Rightarrow \left(\theta \right)_{1}+\left(\theta \right)_{2}=\left(cos\right)^{- 1}\left(\right.0\left.\right)=90^\circ $
So, angle between the velocity vectors of the two particles after the collision is 90°.
Correct option (3)

Given that mass of each particle $=m$
initial velocity of one moving particle $=v$
initial velocity of other particle $=0$ (because it is stationary)
Let after collision,
One particle moves with velocity $v_{1}$ with angle $\theta _{1}$ w.r.t. $x-$ axis,
and other particle moves with velocity $v_{2}$ with angel $\theta _{2}$ w.r.t. $x-$ axis.
Now, by momentum conservation in $x-$ direction
(initial momentum) along $x-$ axis. = (final momentum) along $y-$ axis
$\left(\right.p_{i}\left(\left.\right)_{x - a x i s}=\left(\right.p_{f}\left(\left.\right)_{x - a x i s}$
$\Rightarrow mv+m\left(\right.0\left.\right)=mv_{1}cos\left(\theta \right)_{1}+mv_{2}cos\left(\theta \right)_{2}$
$\Rightarrow v=v_{1}cos\left(\theta \right)_{1}+v_{2}cos\left(\theta \right)_{2}...\left(\right.1\left.\right)$
Now, by momentum conservation in $y-$ direction
$\left(\right.p_{i}\left(\left.\right)_{y - a x i s}=\left(\right.p_{f}\left(\left.\right)_{y - a x i s}$
$\Rightarrow m\left(\right.0\left.\right)+m\left(\right.0\left.\right)=mv_{1}sin\left(\theta \right)_{1}-mv_{2}sin\left(\theta \right)_{2}$
$\Rightarrow 0=v_{1}sin\left(\theta \right)_{1}-v_{2}sin\left(\theta \right)_{2}...\left(\right.2\left.\right)$
and by law of conservation of kinetic energy
$\left(\right.Kineticenergy\left(\left.\right)_{b e f o r e c o l l i s i o n}=\left(\right.Kineticenergy\left(\left.\right)_{a f t e r c o l l i s i o n}$
$\Rightarrow \frac{1}{2}mv^{2}+\frac{1}{2}m\left(\right.0\left(\left.\right)^{2}=\frac{1}{2}mv_{1}^{2}+\frac{1}{2}mv_{2}^{2}$
$\Rightarrow v^{2}=v_{1}^{2}+v_{2}^{2}...\left(\right.3\left.\right)$
Addition of square of eq. (1) and eq. (2)
$\Rightarrow v^{2}+0^{2}=\left(\right.v_{1}cos\left(\theta \right)_{1}+v_{2}cos\left(\theta \right)_{2}\left(\left.\right)^{2}+\left(\right.v_{1}sin\left(\theta \right)_{1}-v_{2}sin\left(\theta \right)_{2}\left(\left.\right)^{2}$
$\Rightarrow v^{2}=v_{1}^{2}cos\theta _{1}^{2}+v_{2}^{2}cos\theta _{2}^{2}+2v_{1}v_{2}cos\theta _{1}cos\theta _{2}$ $+v_{1}^{2}sin\theta _{1}^{2}+v_{2}^{2}sin\theta _{2}^{2}-2v_{1}v_{2}sin\theta _{1}sin\theta _{2}$
$\Rightarrow v^{2}=v_{1}^{2}\left(\right.cos\theta _{1}^{2}+sin\theta _{2}^{2}\left.\right)+v_{2}^{2}\left(\right.cos\theta _{2}^{2}+sin\theta _{2}^{2}\left.\right)$
$2v_{1}v_{2}\left(\right.cos\left(\theta \right)_{1}cos\left(\theta \right)_{2}-sin\left(\theta \right)_{2}sin\left(\theta \right)_{2}\left.\right)$
$\Rightarrow v^{2}=v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}\left(\right.cos\left(\theta \right)_{1}cos\left(\theta \right)_{2}-sin\left(\theta \right)_{1}sin\left(\theta \right)_{2}\left.\right)$
Using eq. (3)
$\Rightarrow v_{1}^{2}+v_{2}^{2}=v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}\left(\right.cos\left(\theta \right)_{1}cos\left(\theta \right)_{2}-sin\left(\theta \right)_{1}sin\left(\theta \right)_{2}\left.\right)$
$\Rightarrow 2v_{1}v_{2}cos\left(\right.\left(\theta \right)_{1}+\left(\theta \right)_{2}\left.\right)=0$
$\Rightarrow cos\left(\right.\left(\theta \right)_{1}+\left(\theta \right)_{2}\left.\right)=0$
$\Rightarrow \left(\theta \right)_{1}+\left(\theta \right)_{2}=\left(cos\right)^{- 1}\left(\right.0\left.\right)=90^\circ $
So, angle between the velocity vectors of the two particles after the collision is 90°.
Correct option (3)