Q.
Consider the system shown in figure with $m_{1}=20.0 \,kg$, $m_{2}=12.5 \,kg , R=0.200 \,m$, and the mass of the pulley $M=10.0 \, kg$. Object $m_{2}$ is resting on the floor, and object $m_{1}$ is $4.00 \,m$ above the floor when it is released from rest. The pulley axis is frictionless. The cord is light, does not stretch, and does not slip on the pulley. The time interval (in s) required for $m_{1}$ to hit the floor is ___.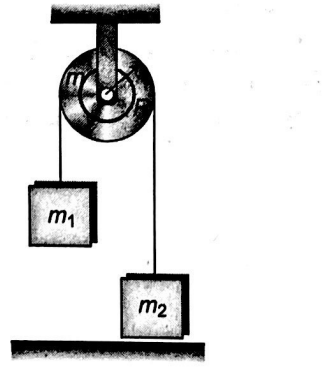
System of Particles and Rotational Motion
Solution:

