Q.
Consider the system shown in figure. The pulley and the string are light and all the surfaces are frictionless. The tension in the string is (take g = 10 m s-2)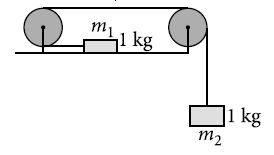
Solution:
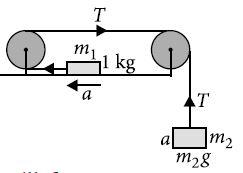
If a is acceleration of m2, then from fig.
$m_{2}g-T=m_{2}a\quad\quad\quad\quad\quad\quad\quad...\left(i\right)$
and T $=m_{1}a=1a\quad\quad\quad\quad\quad\quad...\left(ii\right)$
From $\left(i\right), m_{2} g - T = m_{2}a$
1 g - m$_{1}$a = m$_{2}$a
1 g = $\left(m_{1} + m_{2}\right)a = \left(1 + 1\right)a$
$a=\frac{g}{2}=\frac{10}{2}=5m s^{-2}$
$\therefore \quad T=m_{1}a=1 \times$ 5 = 5 N