Question

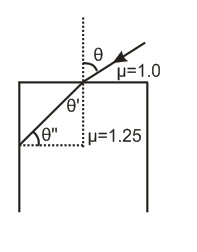
Consider the situation shown in the figure. Here $\theta $ is the maximum angle for which the light suffers total internal reflection at the vertical surface. Then $sin \theta $ will be:-

Answer 1

The critical angle for this case is
$\theta ^{''} = \text{sin}^{-1} \frac{1}{1 \text{.} 2 5} = \text{sin}^{-1 \, } \frac{4}{5}$
or, $\text{sin} \theta ^{''} = \frac{4}{5}$
Since $\theta ^{''} = \frac{\pi }{2} - \theta ^{'} \text{,}$ we have $\text{sin} \theta ^{'} = \text{cos} \theta ^{''} = 3 / 5 \text{.}$ From Snell's law,
$\frac{\text{sin } \theta }{\text{sin } \theta ^{'}} = 1 \text{.} 2 5$
or, $\text{sin} \theta = 1 \text{.} 2 5 \times \text{sin} \theta ^{'}$
$= 1 \text{.} 2 5 \times \frac{3}{5} = \frac{3}{4}$
or, $\theta = \text{sin}^{-1} \frac{3}{4}$ .
If $\theta ^{''}$ is greater than the critical angle, $\theta $ will be smaller than this value. Thus, the maximum value of $\theta $ , for which total reflection takes place at the vertical surface, is $\sin ^{-1}(3 / 4)$.