Q.
Consider the situation shown in figure. The elevator is going up with an acceleration of $2.00 \,m / s ^{2}$ and the focal length of the mirror is $12.0 \,cm$. The entire surfaces are smooth and the pulley is light. The mass-pulley system is released from rest (with respect to the elevator) at $t=0$ when the distance of $B$ from the mirror is $42.0\, cm$. Find the distance (in cm) between the image of the block $B$ and the mirror at $t=0.200 \,s$. Take $g=10 \,m / s ^{2}$.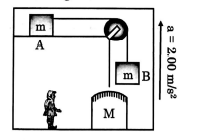
Ray Optics and Optical Instruments
Solution:
